Background
Uncertainty may cause severe consequences or failures if not dealt with properly, and has become an inevitable topic in many research fields such as mechanical design, operations research, networked infrastructure planning, and so on.The goal of robust optimization is to find a solution that is both optimal and insensitive to uncertainty that may exist in parameters and design variables. Since Taguchi proposed the concept of RO, numerous methods and approaches have been published in the literature.
Generally speaking, there are two categories of RO approaches according to how to model uncertainty: probability based and interval based. The former group uses probabilistic information of the design variables and parameters, usually mean and variance, to find robust solutions that are not or least sensitive to those uncertainties. However, this type of approaches is less practical, especially in the early stage of the design procedure, in the sense that establishing accurate probability distributions usually requires numerous history data or experiments in advance. On the contrary, interval based approaches simply require the nominal value (i.e., most likely value) and lower and upper bounds of the uncontrollable uncertainty within which uncertain parameters can vary.
RO approaches have been applied to solve many well-known optimization problems, including linear programming (LP), quadratically constrained quadratic programming, nonlinear optimziationprogramming, and mixer integer programming. etc.
Student
Jiahua Zhou, Shuo Cheng
Platform
Matlab
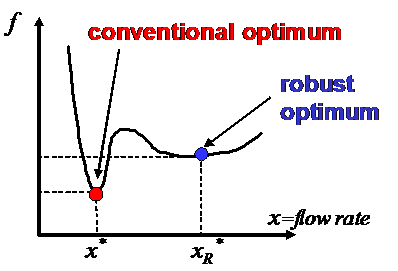
Fig. 1. Robust Optimization Illustration
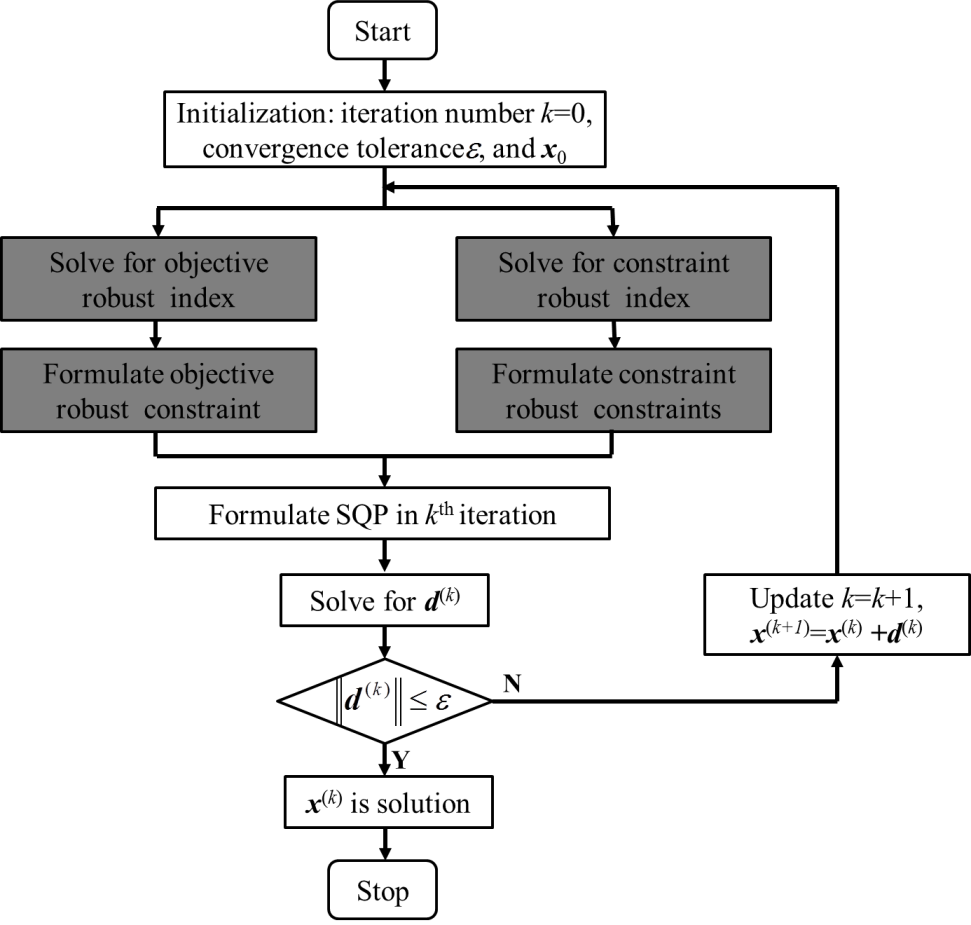
Fig. 2. Sequential Quadratic Programming for Robust Optimization with Interval Uncertainty
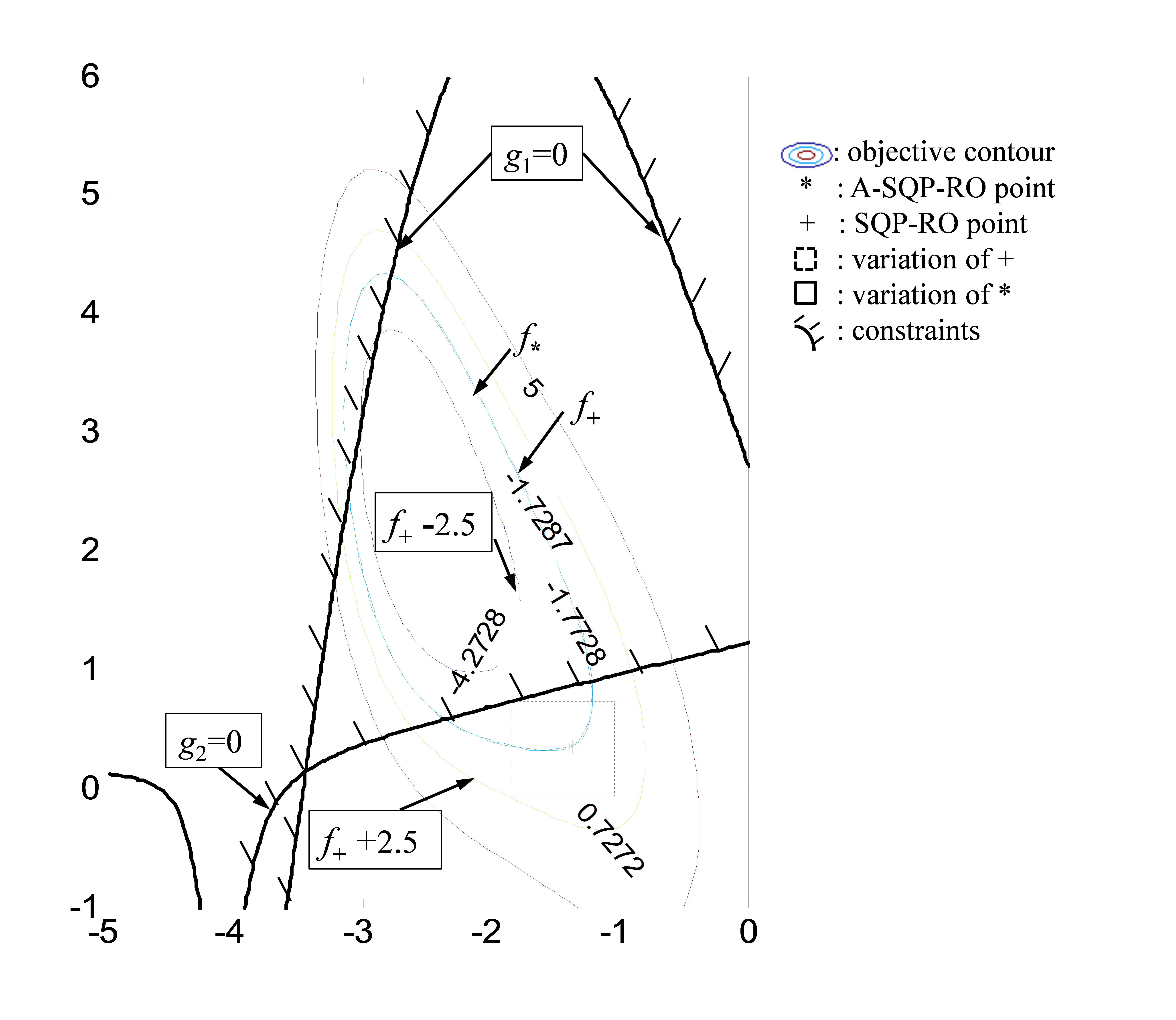
Fig. 3. Result of Advanced SQP-RO appraoch
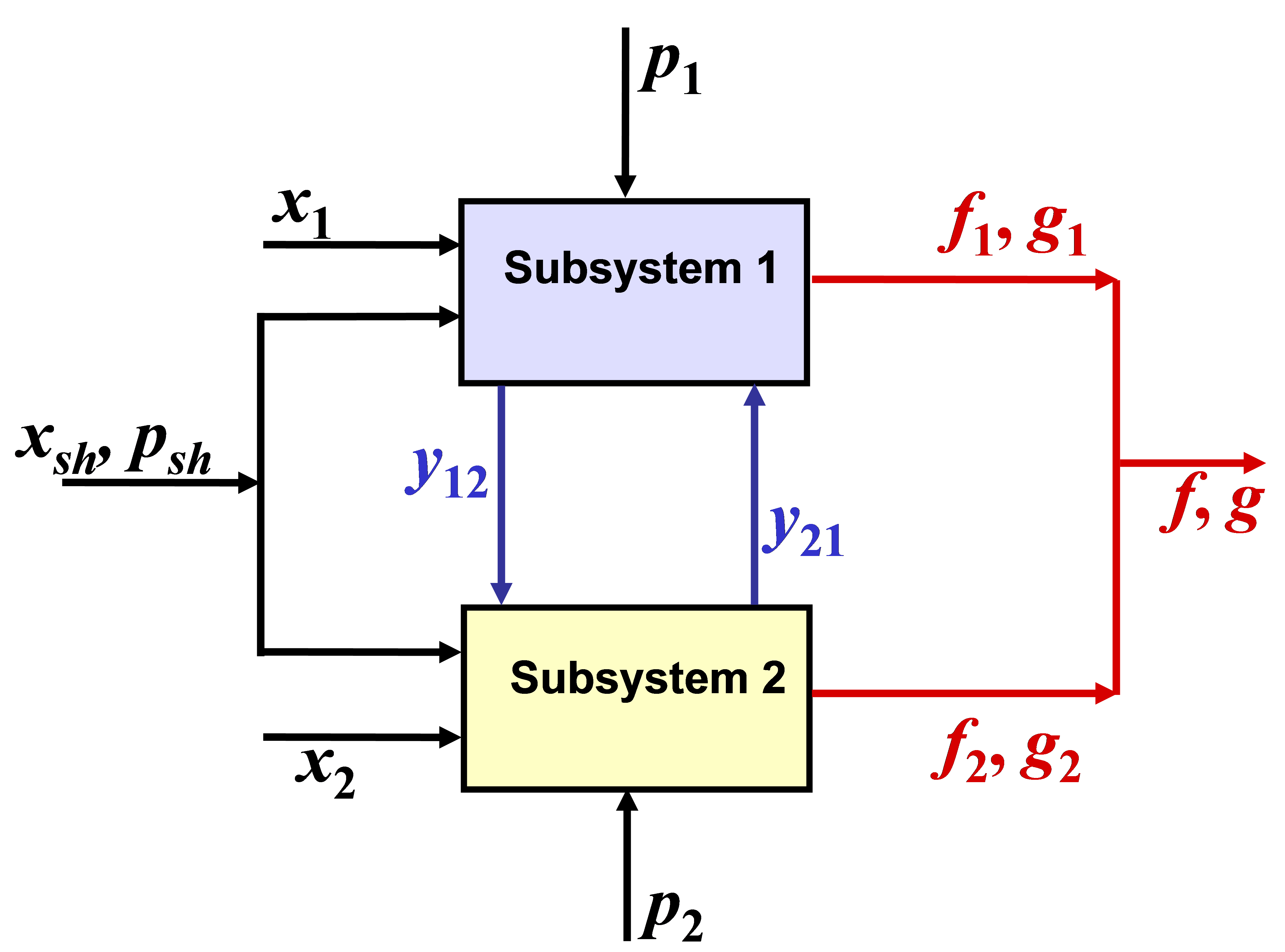
Fig. 4. Multi-Discipline Optimization
Ongoing Topics
- · Algorithm development of MDO methods
- · Study of Modeling uncertainty of MDO